信息存储

16进制表示法

一个字节可以用两个十六进制数字来表示。（一个字节占8位，16进制一个符号占4位，所以一个字节可以用两个16进制符号表示）

字数据大小

**每台计算机都有一个字长(word size)，指明指针数据的标称大小(nominal size)。**因为虚拟地址是以这样的一个字来编码的，所以字长决定的最重要的系统参数就是虚拟地址空间的最大大小。也就是说，对于一个字长为w位的机器而言，虚拟地址的范围为 0~2^w-1^，程序最多访问 2^w^ 个字节。

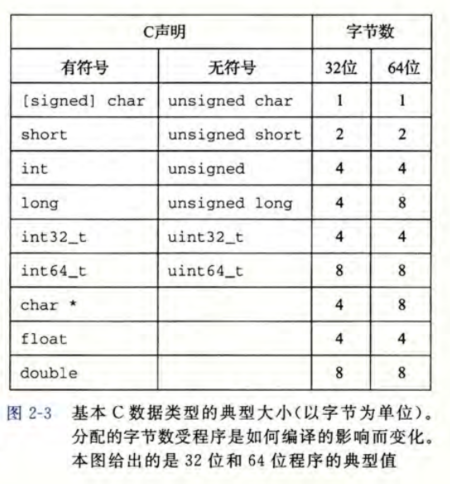
image-20211104142407807 image-20211007171430041

寻址和字节顺序

对于跨越多字节的程序对象，我们必须建立两个规则：这个对象的地址是什么，以及在内存中如何排列这些字节。

排列表示一个对象的字节有两个通用的规则：

  • 小端法（little endian）：最低有效字节在最前面的方式
  • 大端法（big endian）：最高有效字节在最前面的方式
image-20211104141630945

如下代码为使用强制类型转换来访问和打印不同程序对象的字节表示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, size_t len){
	size_t i;
	for(i = 0; i < len; i++)
		printf(" %.2x", start[i]);
	printf("\n");
} 

void show_int(int x){
	show_bytes((byte_pointer) &x, sizeof(int));
}

void show_float(int x){
	show_bytes((byte_pointer) &x, sizeof(float));
}

void show_pointer(int x){
	show_bytes((byte_pointer) &x, sizeof(void *));
}
image-20211104141712311

过程 show_int、show_float 和 show_pointer 展示了如何使用程序 show_bytes 来 分别输出类型为 int、float 和 void* 的 C 程序对象的字节表示。可以观察到它们仅仅传递给 show_bytes 一个指向它们参数 x 的指针 &x， 且这个指针被强制类型转换为“unsigned char * ”。 这种强制类型转换告诉编译器，程序应该把这个指针看成指向一个字节序列，而不是指向一个原始数据类型的对象。然后，这个指针会被看成是对象使用的最低字节地址。

这些过程使用 C 语言的运算符 sizeof 来确定对象使用的字节数。一般来说，表达式sizeof(T)返回存储一个类型为T的对象所需要的字节数。使用 sizeof 而不是一个固定的值，是向编写在不同机器类型上可移植的代码迈进了一步。

1
2
3
4
5
6
7
8

void test_show_bytes(int val){
	int ival = val;
	float fval = (float) ival;
	int *pval = &ival;
	show_int(ival);  //02 00 00 00
	show_float(fval);  //02 00 00 00
	show_pointer(pval);  //dc fd 62 00 00 00 00 00
}

通过试验可以看到Windows是小端法机器

int 和 float除了字节顺序外，在所有机器上得到的结果都是相同的，但是指针却是完全不同，不同的机器/操作系统使用不同的存储分配规则。

位运算

==位运算符：&、 |、^、 ~==
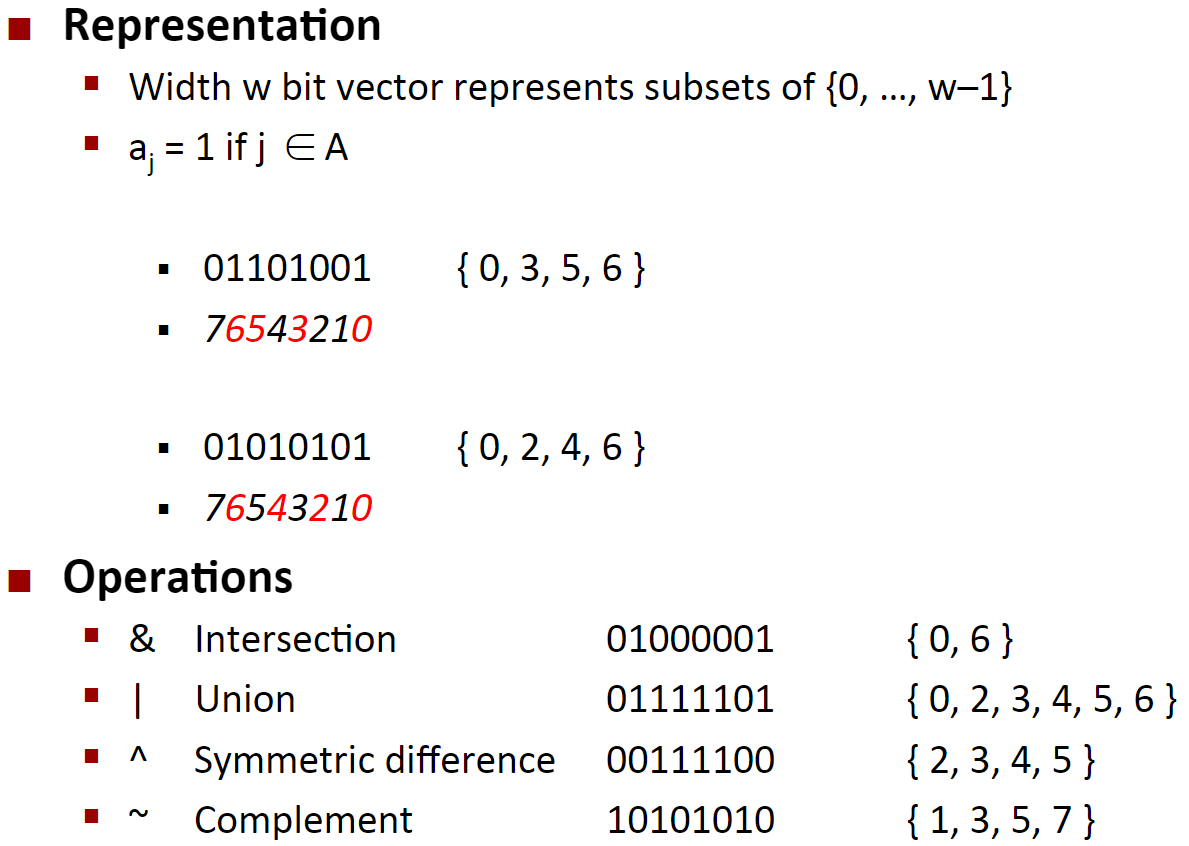
image-20211007185406725

C语言的一个很有用的特性就是它支持按位布尔运算。事实上，我们在布尔运算中使用的那些符号就是 C语言所使用的：| 就是 OR（或），& 就是 AND（与）， ~就是 NOT（取反）， 而 ^ 就是 EXCLUSIVE-OR（异或）。 这些运算能运用到任何“整型”的数据类型上。以下是一些对 char 数据类型表达式求值的例子：

image-20211104143338391

正如示例说明的那样，确定一个位级表达式的结果最好的方法，就是将十六进制的参数扩展成二进制表示并执行二进制运算，然后再转换回十六进制

位运算都先转换成二进制进行运算
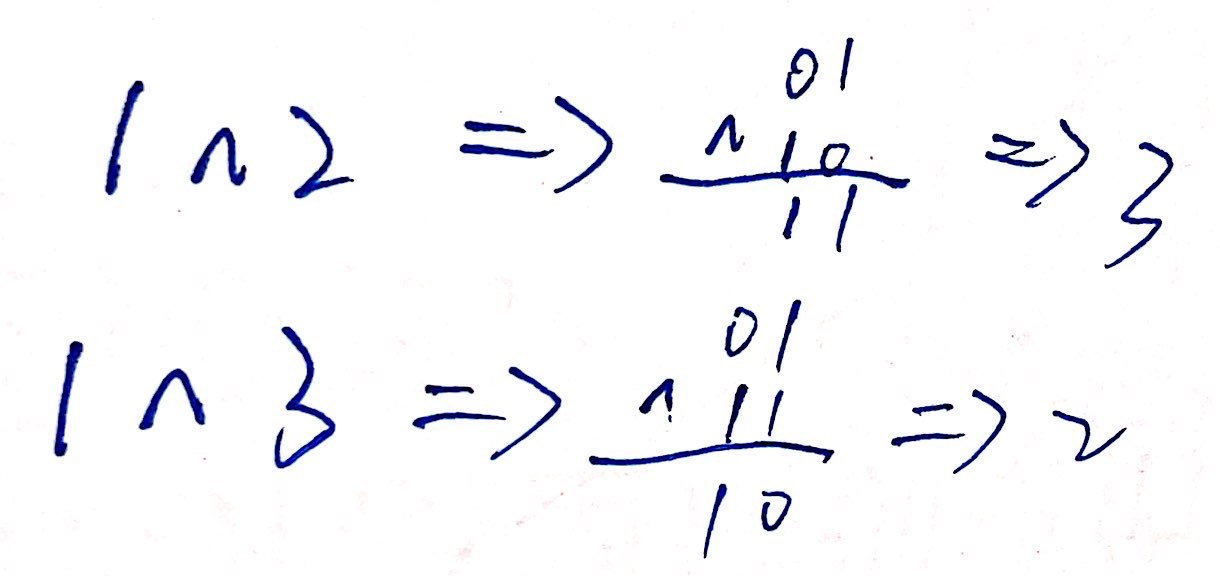
image-20210928192525428
掩码运算

位级运算的一个常见用法就是实现掩码运算，这里掩码是一个位模式，表示从一个字中选出的位的集合。让我们来看一个例子，掩码 OxFF(最低的 8位为1)表示一个字的低位字节。位级运算x&0xFF 生成一个由x的最低有效字节组成的值，而其他的字节就被置为0。比如，对于x=0x89ABCDEF，其表达式将得到0x000000EF。表达式~0 将生成一个全1的掩码，不管机器的字大小是多少。尽管对于一个 32 位机器来说，同样的掩码可以写成0xFFFFFFFF，但是这样的代码不是可移植的。

逻辑运算

==逻辑运算符： &&、 ||、 !==

image-20211007185421214

位移运算

左移运算：x<<k ， x向左移动k位，丢弃最高的k位，并在右端补k个0

右移运算：x>>k ，机器智齿两种形式的右移：逻辑右移和算数右移

  • 逻辑右移：在左端补k个0
  • 算数右移：在左端补k个最高有效位的值
image-20211104143823024

与C相比，Java对于如何进行右移有明确的定义。表达是x>>k会将x算数右移k个位置，而x>>>k会对x做逻辑右移。

image-20211104144055492

整数表示

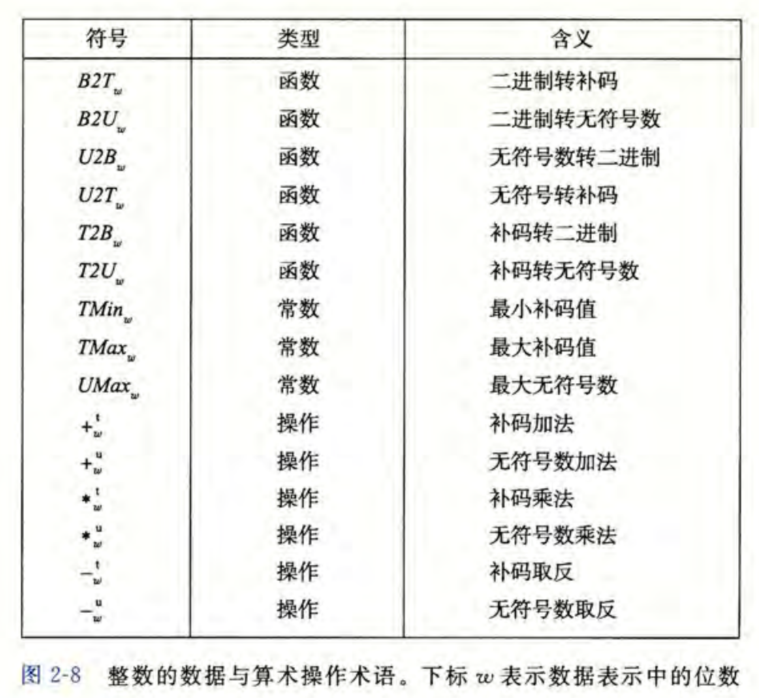
image-20211104144603029

无符号数的编码

image-20211104144643881

补码编码

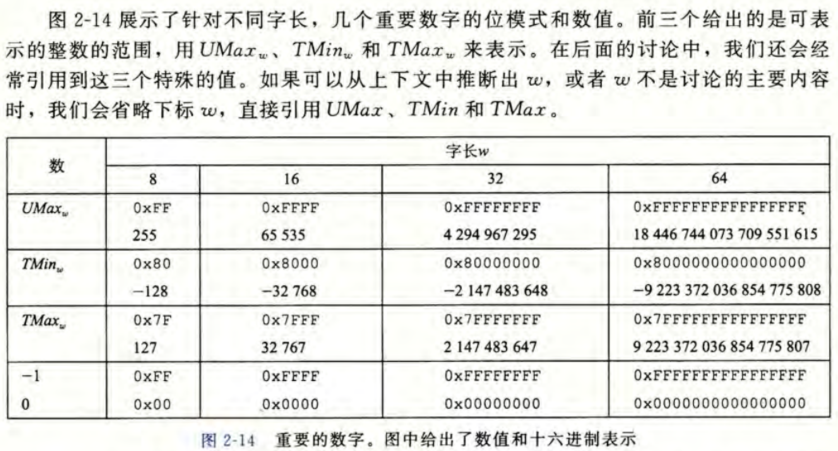
image-20211104144717757 image-20211104144746839

有符号数和无符号数之间的转换

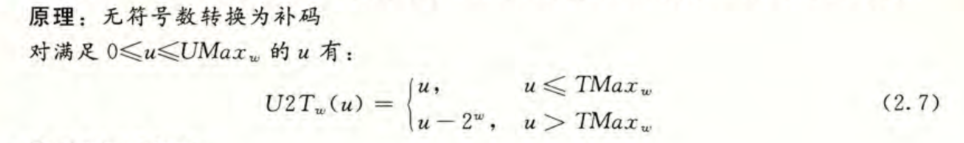
image-20211104145052985 image-20211104145112226

0-1 -> UMax

1

printf("%u\n",0-1);  //4294967295
image-20211007151050453

扩展一个数字的位表示

在采用补码表示的 32 位大端法机器上运行这段代码时，打印出如下输出：

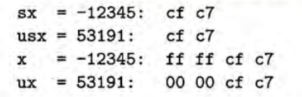
image-20211104145632999

我们看到，尽管 -12345 的补码表示和 53191 的无符号表示在 16 位字长时是相同的，但是在 32 位字长时却是不同的。特别地，-12345 的十六进制表示为 0XFFFFCFC7，而 53191 的十六进制表示为 0x0000CFC7，前者使用的是符号扩展——最开头加了 16 位，都是最高有效位 1。表示为十六进制就是 0xFFFF，后者开头使用16个0来扩展，表示为十六进制就是 0x0000。

图 2-20 给出了从字长 w=3 到 w=4 的符号扩展的结果。位向量[101]表示值-4+1=-3。对它应用符号扩展，得到位向量[1101]，表示的值-8+4+1=-3。我们可以看到，对于 w=4，最高两位的组合值是-8+4=-4，与w=3时符号位的值相同。类似地，位向量[111]和[1111]都表示值-1。

image-20211104145848026

截断数字

截断无符号数
image-20211104150511824
截断补码数值
image-20211104150531549

整数运算

无符号加法

原理

image-20211104152023915

检测无符号数加法中的溢出

image-20211104152056173 

1
2
3
4
5

//无符号加法是否溢出， 如果参数x和y相加不会产生溢出，这个函数就返回1
int uadd_ok(unsigned x, unsigned y){
	unsigned sum = x + y;
	retrun sum >= x;
}
阿贝尔群
image-20211104153404824

补码加法

image-20211104152221839

检测补码加法中的溢出

image-20211104153553753 

1
2
3
4
5
6
7
8

//补码加法是否溢出，参数x和y相加不会产生溢出，这个函数就返回1 
int tadd_ok(int x, int y){
	int sum = x + y;
	int neg_over = x < 0 && y < 0 && sum >= 0;
	int pos_over = x >= 0 && y >= 0 && sum < 0;
	
	return !neg_over && !pos_over;
}

补码的非

image-20211104153915800 

1
2
3
4
5
6
7

x -> -x
-6 -> 6
      1010
 ~    0101
 +1   0001
 =============
      0110(6)

无符号乘法

image-20211104154545655 

1
2
3
4
5
6
7
8
9

     1001
*    1101
=============
     1001
    0000
   1001
+ 1001
=============
  1110101

补码乘法

image-20211104154612198 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

-2 * -3 = 6
如下做无符号乘法运算:
     1101(13)
*    1110(14)
=============
     0000
    1101
   1101
+ 1101
=============
 10110110
十六进制:0xb6
仅看低位:0110(6)

乘以常数

**在大多数机器上，整数乘法指令相当慢，需要10个或者更多的时钟周期，然而其他整数运算（例如加法、减法、位级运算和位移）只需要1个时钟周期。**因此，编译器使用了一项重要的优化，试着用位移和加法运算的组合来代替乘以常数因子的乘法。

image-20211104161201748

除以2的幂

在大多数机器上，整数除法要比整数乘法更慢——需要30个或者更多的时钟周期。

除以2的幂的无符号除法

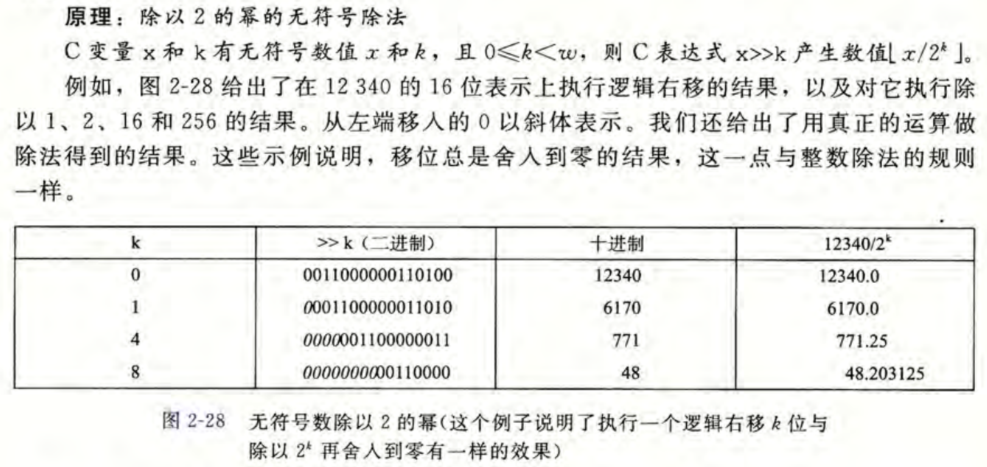
image-20211104162603412

除以2的幂的补码除法，向下舍入

image-20211104162630960

image-20211104162652701

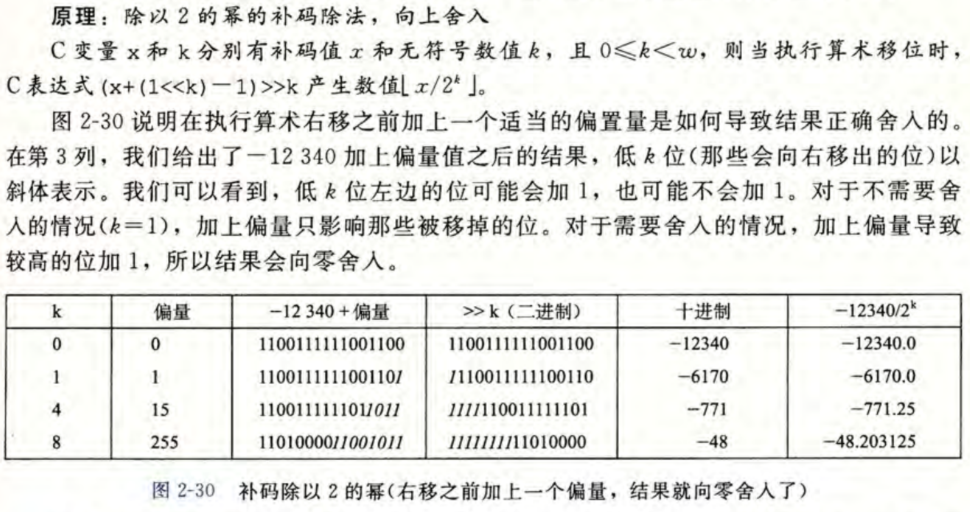
除以2的幂的补码除法，向上舍入

可以通过在移位之前“偏置（biasing)”这个值，来修正这种不合适的舍入。

image-20211104162717112

浮点数

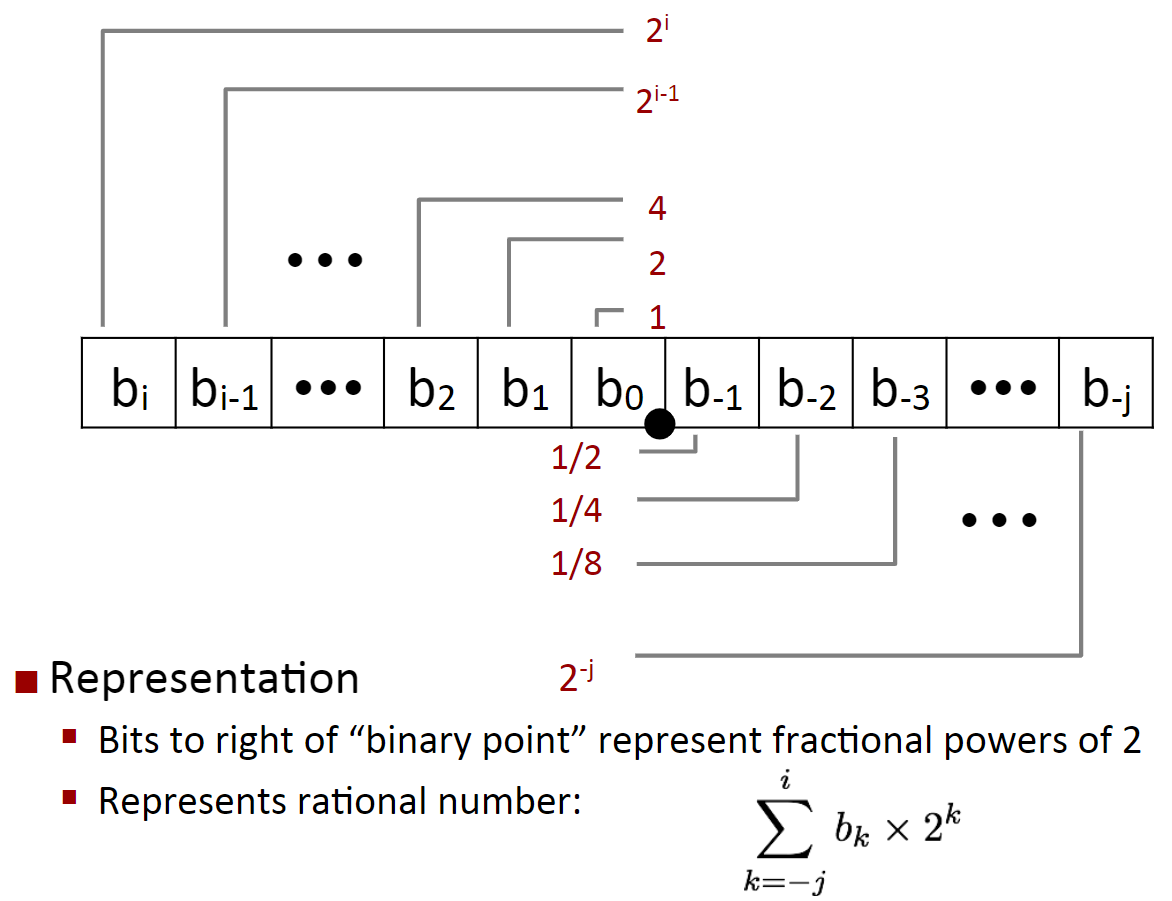
image-20211007191620204

二进制小数

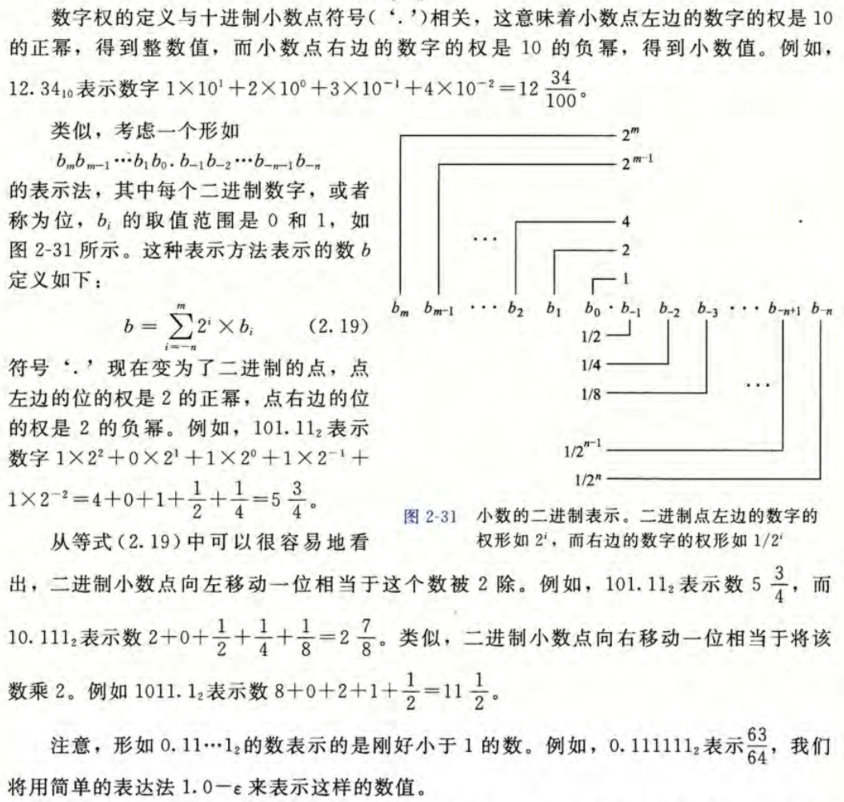
image-20211104163524157

IEEE浮点表示

image-20211104164525964

image-20211104164630433

image-20211104164752484

image-20211104164806055

规格化示例
image-20211007193640164

IEEE754浮点数阶码为什么需要偏置bias

主要原因是使指数以无符号形式存储

以单精度浮点型float为例，e由8bit二进制原码（无符号）表示，但这样的小数不能表示 （-1，1）中的数，因为阶码总是正数。那怎么办呢？用补码表示e？麻烦，还要考虑符号！

所以不如减去一个偏置量127（为什么是127？不是128？https://blog.csdn.net/weixin_43891234/article/details/114693495），这样就能表示负的E（如果没有偏置，那么e=E），此时 E = e -127，而e范围为（0000 0001 - 1111 1110 即 1-254，0000 0000和1111 1111单独用来表示非规格化值），最终E 的范围（1-127 到 254-127）=（-126，127）。

数字示例

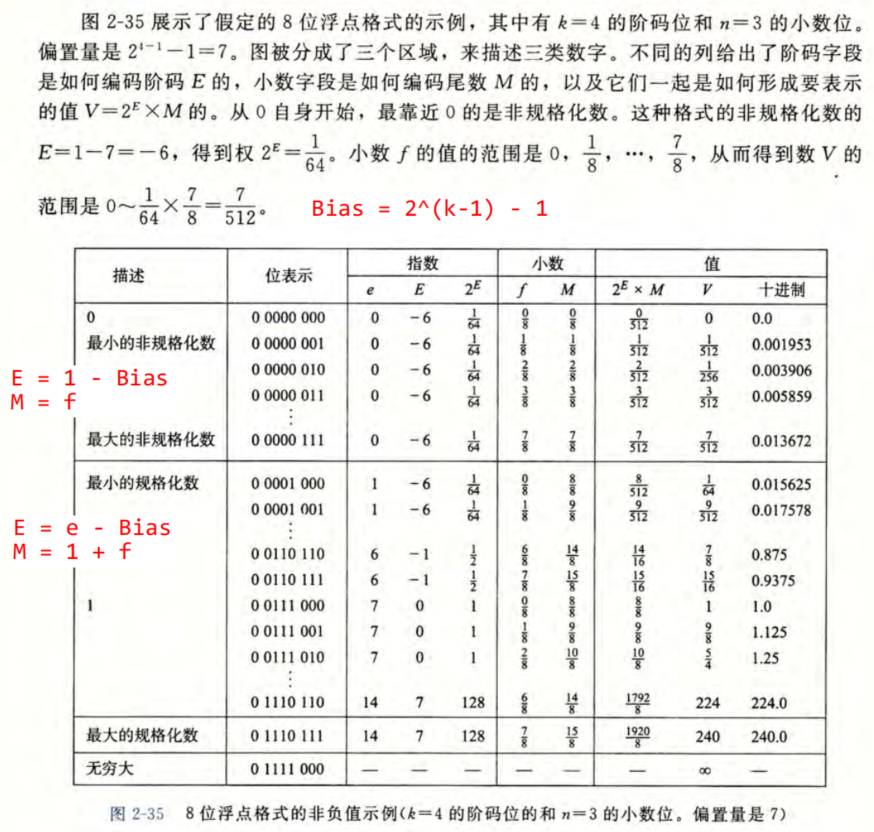
image-20211104170928333

image-20211104171003897

整数值转换成浮点形式 书P82（操作见上面的规格化示例）

image-20211104173052940

舍入

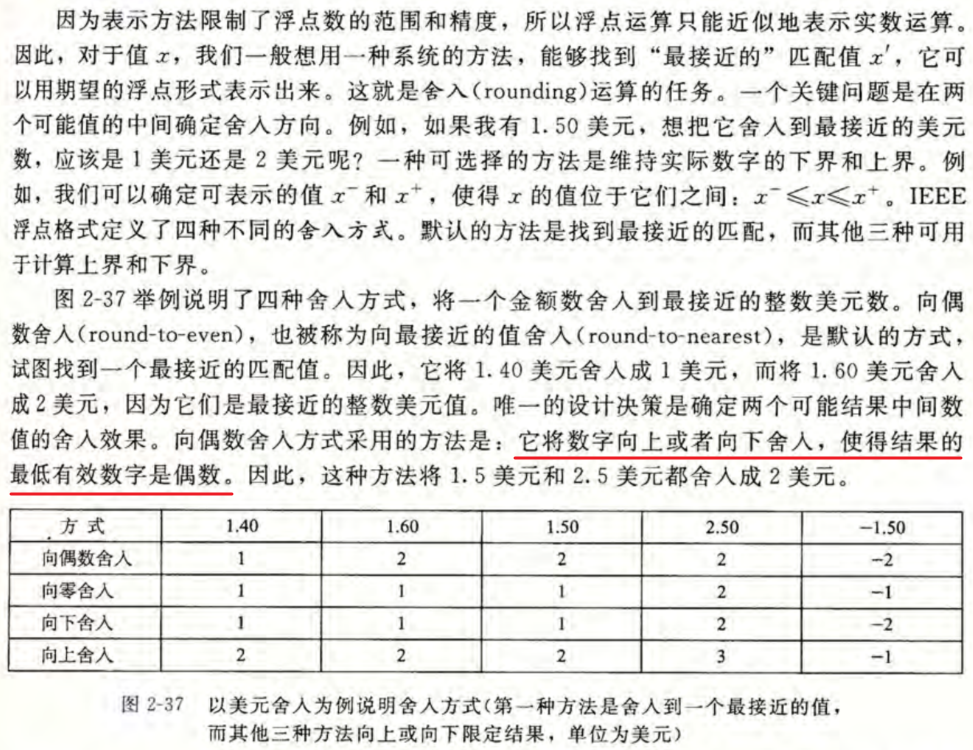
image-20211104173232060

image-20211104173152699

浮点运算

总结一下：

浮点运算与我们平常做的运算类似

满足单调性